2020/01/30 タグを追加しました
1. 【まとめ】投資にすぐ効く!統計学で知っておくべきたった5つのポイント(導入動画付き)
一時期、「統計学は最強の学問である」などの統計学本が流行ったり、データサイエンティストが大注目されたりする時期(今も?)があったりしたかと思います。
そして、いまがブームかはさておいて、投資でも統計学はとても「使える」学問のひとつです。
かく言う私も、理系出身ではありませんが、確率や統計は高校時代から大好きな科目であり、大学時代や社会人時代もそれらを活かして、研究や仕事、そして、投資をしてきました。
とはいえ、「数字や数式が大の苦手!できれば勉強もしたくない…」という方は比較的多いかと思います。
そこで、今回の記事では、統計学好きの私が、投資を実践する中で、最も大切だと感じたコトを5つだけに絞ってまとめておきました。
統計学にいままで縁のなかった方も、本記事の知識を是非投資の成功につなげてもらえたらと思います。
2. 投資にすぐ効く5つの統計学知識
それでは早速、投資に効く5つの統計学のポイントについて、ひとつひとつ解説していきたいと思います。
①あくまで「過去」を扱う学問である
まずは、統計学が何を大元の材料として発展してきたモノなのか考えてみましょう。
それは、「過去のデータ」です。
株価の値動きにせよ、人口動態にせよ、webサービスの利用データにせよ、これがなくては、統計学は基本的に成立しません。
そして、近年統計学やデータサイエンスが注目される理由の一つには、人間がつくり出すデータ量が爆発的に増えているので、価値を生み出す可能性が広がっているというということがあります。
そのため、統計の考え方を使って生み出された情報を使う際には、大前提として理解しておくべき大切なことがあります。
それは、「未来は過去の延長線上にあるとは限らない!」ということです。
統計学を活用した将来の予測が機能するのは、基本的に、統計で分析した過去データと同じ未来が続く場合だけです。
この点をよくよく理解しておかないと、他人の分析の結果を鵜呑みにしてしまったり、自分の予測で無用な一喜一憂を繰り返してしまったりすることになります。
あくまで、分析の期間の過去と同じ未来が続いた場合に使えるひとつのツールに過ぎないと覚えておきましょう。
②時間や回数を重ねるほど平均に近づく
統計学を専門的に勉強したことがない方でも、「平均」のことはご存知だと思います。
複数の数字を頭数で割り戻した平均身長や平均年収や、株価の一年間の値上がりを複数の銘柄で割り戻した「平均リターン」と呼ばれるものもあります。
このなじみのある平均については、「大数の法則」というものが働いています。
名前が少し仰々しいのですが、なんのことはなく「何度も繰り返せば繰り返すほど、結果は平均に近づいていく」ということだけです。
例えば、表と裏が出る確率が50%ずつのコイントスがわかりやすいでしょう。
あなたが10回繰り返したときより100回繰り返したとき、100回繰り返したときより1000回繰り返したとき、・・・繰り返しの回数が多ければ多いほど、表の出た確率は50%に近づいていきます。
これは、ある意味コイントスと同じ投資でもとても重要です。
例えば、あなたが過去10年間で年平均12-13%のリターンを出しているアメリカのS&P(日本で言う日経平均のようなもの)に投資をしたとしましょう。
仮にわかりやすく1年間の投資を1回とカウントするならば、1年目(1回目)のリターンが平均どおりである確率はとても低いでしょう。
もちろん、マイナスになっていることすら当然にありえます。
しかし、10年目、20年目、30年目…と投資を繰り返すほどに、平均の12-13%に近づく可能性は高まっていきます。
これが、時間を味方にする長期投資が上手くいく理由の一つということになります。
③リターンのばらつきを数字の大きさで知ることができる
投資にとても役立つ統計学の概念の一つとして「標準偏差」があります。
言葉が難しいと思われるかもしれませんが、単に「ばらつきの大きさ」を数字で示したものです。
(おなじみのテストの偏差値を計算する際にも、同じ考え方を使います。)
また、この概念は、私が本ブログで繰り返し解説している「リスク(リターンのばらつき)」そのものです。
例えば、商品のカテゴリごとに各銘柄の特定期間のリターンの数字を使って、ばらつき具合を計算することができます。
一例としては、モーニングスターなどのサイトで、投資信託ごとの標準偏差を確認できます。
また、下図のように、ばらつきが小さいほどどの銘柄や商品を選んでも、平均に近いリターンが得られる可能性が高まります。そして、ばらつきが大きい場合には、平均より大きいリターンが得られやすい代わりに、平均を下回る可能性(さらに、単に下回るだけでなく、リターンがマイナスになる可能性)も高まります。
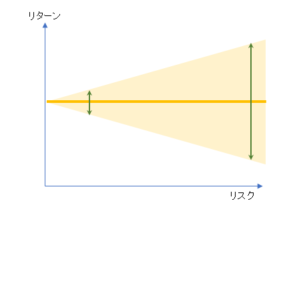
ただし、本ブログでは繰り返しお話している通り、標準偏差(=リスク)の大小はどちらの方が良いというものでは全くありませんので十分注意しましょう。
あくまで、自分の投資の目的地と現在地によって、取るべきリスクの大きさが決まってくる、というだけです。
(参考記事)
【保存版:投資とは?】意味も知らずに投資してるやつちょっと来い
標準偏差(=リスク)は、投資商品のリターンの性質と、自分が選ぶべき商品を教えてくれる大切な数字なのです。
④複数の投資を組み合わせることでリスクを抑えられる
統計と金融の境目のポイントになりますが、複数種類の投資を組み合わせることでリスクを抑えられることも大切なポイントです。
ここでのリスクも、リスク=標準偏差=リターンのばらつきのことを指しています。
(注:「危険性」という意味合いではありません!)
このポイントは、マーコビッツという人が1952年に発表した「現代ポートフォリオ理論」というものに基づいています。
リターンや標準偏差の水準が異なる複数の商品に投資すると、単一の投資商品に投資したときと比べて、リターンを維持したまま、標準偏差(リターンのばらつき)を下げられるというものです。
要は、複数の商品を組み合わせて分散投資するだけで、平均的な水準として狙っていたリターンを得られる可能性が高まる!ということです。
なお、分散投資をかごに盛った卵に例える方もいますが、個人的にはあまり好きではありません。
それは、投資に失敗してかごの卵が一気に割れてしまうイメージが「危険性」という意味でのリスクを想起させてしまうからです。
あくまで、分散投資で低下するのは「リターンのばらつき」という意味でのリスクなのです。
⑤平均や標準偏差は投資するヒトの感覚と乖離する事が多い
最後は、統計学の内容を直接解説するものではありませんが、大切な数字との付き合い方についてお話したいと思います。
それは、ここまででお話してきた平均や標準偏差などの概念は実際に自分の資金で投資するヒトの感覚と合わないことが多いということです。
どれも理論や計算としては正しいものの、実は人間の認知やそのバイアスと合わない事が多いのです。
例えば、あなたが年間リターン12%を目指して、ある株式へ投資をはじめたところを想像してみましょう。
本当に自分のお金を、それも、自分にとって大きめの金額を投じているところを想像してください。
投資した後の1年間、毎月毎月どんなことが起こりそうでしょうか?
あなたが想像したのはこんなイメージではないでしょうか?
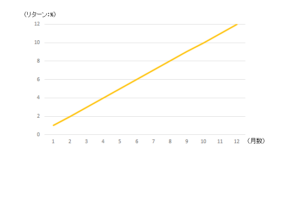
年間12%想定なので、毎月毎月1%のリターンが上がって、無事トータル12%のリターンで年末を迎えることができました!おめでとうございます!
ところが、残念なことに預金や債券の利息を除いて、こういった直線的なリターンが出ることはほとんどありません。
例えば、株式の標準偏差が20-40くらいだとすると、最初の年にマイナスのリターンになることも当然ありますし、それが数年連続しても特に不思議はありません(=分析に使った過去のデータから外れたことが起きているとは言えません)。
しかし、それを知らない人、あるいは、ある程度知っている人でさえ(!)、自分が勝手に想像していた真っ直ぐな直線から下回ってしまうと、精神的に大きな影響を受けます。
そして、価格変動が気になって他のことに手がつかなくなったり、10年以上の長期投資のつもりだったものを途中で手放してしまったりします。
これは理屈だけをいくら勉強しても対処できるものではなく、投資の勉強と実践を繰り返さないと対処できないものです。
ちなみに、私は初めて投資をスタートするまで、このことは知りませんでしたので、本格的な投資の前にこの情報を知った方は相当有利にゲームを進めることができると思います。
なお、余談ですが、平均や期待値、標準偏差などの概念は、実は人間の歴史でとても日が浅いもののひとつです。(先程のポートフォリオ理論も1950年代ですね。)
それまでは、自分の期待する通りのことが起きないとき、単なる運だとか、神様の差配だとかで出来事を解釈するのが普通だったのです。
そういった意味でも、現代でもヒトの感覚に合わないのは当然かもしれません。
3. まとめ
①統計学はあくまで「過去」を扱う学問である
②時間や回数を重ねるほど平均に近づく:大数の法則
③リターンのばらつきを数字の大きさで知ることができる:標準偏差
④複数の投資を組み合わせることでリスクを抑えられる:現代ポートフォリオ理論
⑤平均や標準偏差は投資するヒトの感覚と乖離する事が多い
いかがだったでしょうか?
数字や統計が嫌い方も、必要なポイントを抑えて、正しい投資の道を進んでいってもらえたら嬉しく思います。






















コメントを残す
コメントを投稿するにはログインしてください。